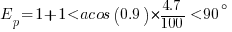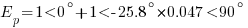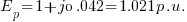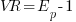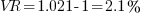The impedance of a transformer limits the fault current through the transformer in the event of a fault. On the downside, it influences the voltage regulation of the transformer. International Standards provide typical impedance of transformers but it is always the design engineer that decide the final value depending on the application of the transformer being procured. Voltage regulation is directly proportional to the transformer impedance. Excessive impedance can cause problems in voltage regulation.
Voltage regulation or plainly regulation is commonly defined as the drop in secondary voltage when a load is applied, but regulation is more correctly defined as the increase in secondary output voltage when the transformer load is disconnected as the rated secondary voltage is the voltage at the transformer secondary terminals when it is loaded at full of its capacity. Thus, the primary voltage is greater than the rated primary voltage at full load.
To calculate transformer voltage regulation VR, let Ep equal the primary voltage and let Es equal the secondary voltage at full load. Using per-unit method of calculation, the per-unit secondary voltage Eswill equal Ep with the load is disconnected. Therefore, the regulation can be expressed by the following equations.
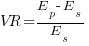
Since
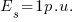
Therefore the equation for voltage regulation could be simplified to become
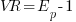
To illustrate this, let us provide an example.
Calculate the voltage regulation of a transformer rated 1250 KVA, 3.3/0.415kV, 4.69%Z at full load of 0.9 PF.
Solution:
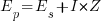
where:
I=secondary full load current
Z=transformer impedance