Harmonic distort the fundamental frequency of the mains voltage waveform which affects the performance of other electrical equipment and creates additional losses and heating.
A total harmonic voltage distortion of 2.5% can cause an additional temperature rise of 4 deg.C in induction motors. In cases where resonance can occur between the system capacitance and reactance at harmonic frequencies, voltage distortion can be even higher.
Capacitive reactance is inversely proportional to the frequency. Harmonic frequencies are multiples of the fundamental frequency which means that capacitive reactance at harmonics frequencies is inversely proportional to the harmonic order number.
This is a clear indication that capacitor banks are highly vulnerable to harmonics as capacitors present low impedance at harmonics frequency currents which could increase the dielectric losses causing overloading leading to eventual failure.
Transformers, cables and switchgear from which the converters are supplied should be de-rated to accommodate the harmonic currents and the extra losses associated with the high frequency ‘skin-effect’.
Industry standards recommends that electric supply equipments for 6-pulse converters must be de-rated by about 10% of the converter full load current and for 12-pulse converters by about 5% of the converter full load rated current.
The order of the harmonic currents that will be present can be predicted mathematically and is given by the formula:
where:
n = order of the harmonics present
k = integers 1, 2, 3, etc
p = pulse number of the converter
Example, for a 6-pulse converter, the harmonic order numbers will be
n = 1 x 6 – 1 = 5
n = 1 x 6 + 1 = 7
n = 2 x 6 – 1 = 11
n = 2 x 6 + 1 = 13
n = 3 x 6 – 1 = 17
n = 3 x 6 + 1 = 19
n = 4 x 6 – 1 = 23
n = 4 x 6 + 1 = 25
n = 5 x 6 – 1 = 29
n = 5 x 6 + 1 = 31
The magnitude of harmonic current is
where:
In= Harmonic current at order n.
I1= Fundamental current
n= harmonic order number5th Harmonic (250 Hz): 20.0% x I1
7th Harmonic (350 Hz): 14.3% x I1
11th Harmonic (550 Hz): 9.1% x I1
13th Harmonic (650 Hz): 7.7% x I1
17th Harmonic (850 Hz): 5.9% x I1
19th Harmonic (950 Hz): 5.3% x I1
23rd Harmonic (1150 Hz): 4.3% x I1
25th Harmonic (1250 Hz): 4.0% x I1
29th Harmonic (1450 Hz): 3.4% x I1
31th Harmonic (1550 Hz): 3.2% x I1, etc
Normally,only up to 50th harmonic is calculated as measuring instruments can only efficiently measure harmonics up to that order.
The equation for harmonic current will be
From the above calculation, a 6-pulse converter theoretically will have a 4.33% more current relative to the fundamental current.
In reality however, harmonics comprises of two components, order harmonics and non-order harmonics. The order harmonics is the one we just calculated above but the non-order harmonics could not be calculated as this is directly affected by the construction of the converter.
As we know that power is directly proportional to the square of the current, 1.04332 = 1.088. This is an 8.8% increase in power consumption compare to the consumption when there are no harmonics currents. It is from this theory that the 10 % de-rating of electrical supply equipment was based on.
References:
Practical Variable Speed Drives and Power Electronics
Malcolm Barnes
Newnes, 2003

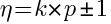
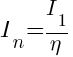
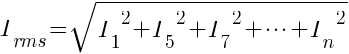
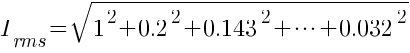
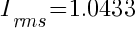
hi sir. I am also an electrical engineer. can you please give me the exact site where i can download the book mentioned above for free. I just recently graduated and passed the board and i want to know more about harmonics. This is Jess again. thank you sir!