From the previous article, the arcing current Ia was calculated from the bolted fault current. With the arcing current already known, the incident energy can then be calculated. To determine the incident energy using the empirically derived equation from NFPA 70E 2015, calculate the log 10 of the normalized incident energy. The following empirical equation [1] is based on data normalized for an arc time of 0.2 second and a distance from the possible arc point to the person of 610 mm.
…..[1]
where:
En = incident energy, normalized for time and distance, J/cm2
Ia = 18.17498605 kA (See Arc Flash – Calculating Arcing Current)
85% x Ia = 15.44873814 kA (Second arcing current)
k1 = −0.792 for open air arcs
k1 = −0.555 for arcs-in-a-box
k2= 0 for ungrounded and high-resistance grounded systems
k2 = −0.113 for grounded systems
G = conductor gap, mm (see Table 2)
From the example in the previous article, the bolted fault is 34.73 kA.
Substituting the given values in [1] where k1 = −0.555 for arcs-in-a-box, and k2 = −0.113 for grounded systems as the transformer is Delta-Wye neutral grounded. G is 25 mm for LV MCC.
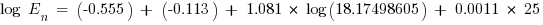
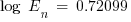
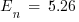 J/cm2
J/cm2
This is the incident energy normalized at 0.2 s arcing time and a working distance of 610 mm.
The normalized incident energy based on the reduced arcing fault current is
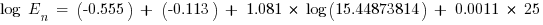
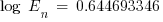
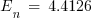 J/cm2
J/cm2
For other values of arcing time and working distance, use the following equation [2].
…..[2]
where:
E = incident energy, J/cm2.
Cf = calculation factor
Cf = 1.0 for voltages above 1 kV.
Cf = 1.5 for voltages at or below 1 kV.
En = incident energy normalized.
t = arcing time, sec.
x = distance exponent from Table D.4.2.
D = distance, mm, from the arc to the person (working distance). See Table 3.