Solution
For the 120 mm2 cable
the series impedance is:
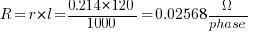
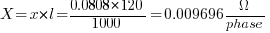
For the 110kW motor
the starting current is:
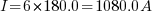
The power factor is:
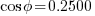 , therefore
, therefore 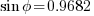
Let us assume the sending voltage remains constant at 400 volts,
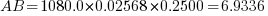 volts/phase
volts/phase
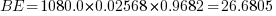 volts/phase
volts/phase
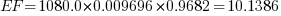 volts/phase
volts/phase
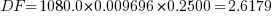 volts/phase
volts/phase
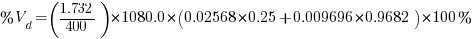
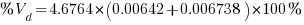
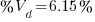
Therefore,
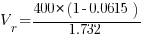
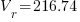 volts/phase
volts/phase
Typical minimum starting voltage for motors is 80% x rated voltage. Since the calculated volt-drop in our example is less than 20%, the motor will accelerate to full speed easily.
In practice, since the actual motor parameters are not known during the design stage, the minimum starting voltage is raised to 85% to provide a factor for safety.
On the next part, we shall be providing more examples for voltage drop calculations.