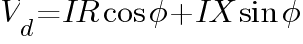Derivation of Voltage Drop Formula
A short cable voltage drop in AC systems is provided by the formula
where:
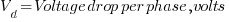
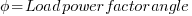
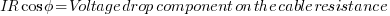
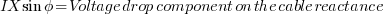
You might be wondering where this formula came from. Actually, this formula is just an approximation. We shall going through the process of deriving this formula to better understand it.
Considering the following vector diagram:
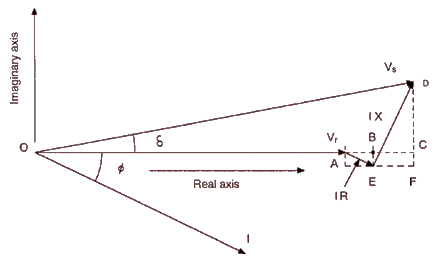
where:
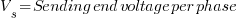
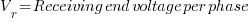
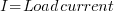
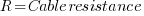
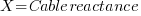
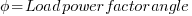
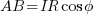
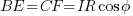
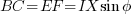
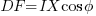
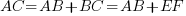
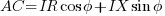
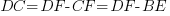
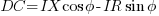
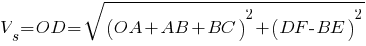
Unless the cable is very long, the imaginary axis component of the voltage is very small compared to the real axis component.
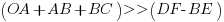
thus the sending end voltage will be
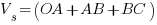
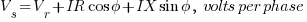
From the above formula, the voltage drop on a per phase basis will be
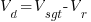
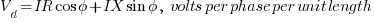
That is how the voltage drop formula was derived.
Normally, voltage drop is expressed as a percentage of the sending end line-to-line voltage. The formula will be
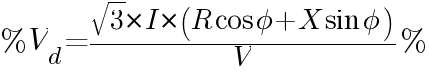
where:
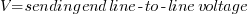
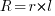
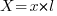
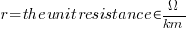
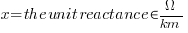
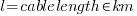
Cable data will be taken from published Vendor data.