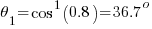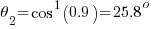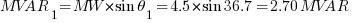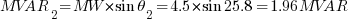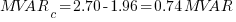Power Factor Correction – MVA Method – Ver Pangonilo, PEE RPEQ

Another application of MVA Method is power factor correction. Consider the diagram below:

$MVA_1 = sqrt{MW^2+{MVAR_1}^2}$ right {(1)}
$MVAR_1 = sqrt{{MVA_1}^2-MW^2}$ right {(2)}

$MVA_2 = sqrt{MW^2+{MVAR_2}^2}$ right {(3)}
$MVAR_2 = sqrt{{MVA_2}^2-MW^2}$ right {(4)}

$MVAR_c = {MVAR_1}-{MVAR_2}$ right {(5)}

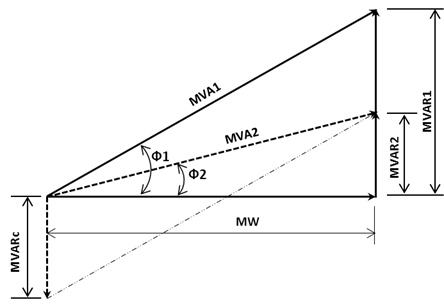
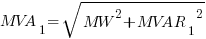
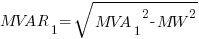
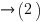
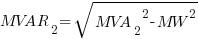
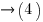
where:MW = real power MVA1 = apparent power (before power factor correction) MVAR1 = reactive power (before power factor correction) MVA2 = apparent power (after power factor correction) MVAR2 = reactive power (after power factor correction) MVARc = Power Factor Capacitor MVAR 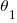= Power Factor (before power factor correction) 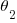= Power Factor (before power factor correction)

Using the above formula, find the size of power factor capacitor to improve the power factor of an industrial plant from o.80 lagging to 0.90 lagging if the maximum demand is 4.5 MW.

Solution:
$theta_1 = {cos^1}(0.8) = 36.7^o$
$theta_2 = {cos^1}(0.9) = 25.8^o$